3학년 2학기 기하 파트에서 처음 배우는 삼각비에 관련된 내용입니다
중등과정에서 배우는 삼각비는 고등과정에서 삼각함수로 연계되는 내용이기 때문에 정확하게 개념을 파악해야 합니다
1. 삼각비란 무엇인가
삼각비는 직각삼각형에서 두 변의 길이의 비를 나타낸 것입니다
닮음인 직각삼각형끼리는 각 변의 길이의 비가 모두 같을 것입니다.(이건 2학년 닮음 파트에서 배웠을 겁니다)
예를 들어

위와 같이 서로 닮음인 세 직각삼각형이 있습니다
삼각비는 직각삼각형에서 두 변의 길이의 비를 나타낸 것이라고 했으므로
크게 3가지 비가 나올 수 있겠네요
위 직각삼각형에서 아래 3가지의 길이비를 구해볼까요?
\begin{equation}1. \; \frac{높이}{빗변} = ? \end{equation}
\begin{equation}2. \; \frac{밑변}{빗변} = ? \end{equation}
\begin{equation}3. \; \frac{높이}{밑변} = ? \end{equation}
답을 공개해 볼까요?
어차피 세 직각삼각형은 모두 닮음이기 때문에 길이비가 모두 같습니다
그렇기 때문에 답은
\begin{equation}1. \; \frac{높이}{빗변} = \frac{3}{5} \end{equation}
\begin{equation}2. \; \frac{밑변}{빗변} = \frac{4}{5} \end{equation}
\begin{equation}3. \; \frac{높이}{밑변} = \frac{3}{4} \end{equation}
이렇게 되겠네요!
수학에서는 앞서 구했던 직각삼각형에서의 세 가지의 길이비의 이름이 있습니다
그것이 바로 sin(사인), cos(코사인), tan(탄젠트) 입니다!
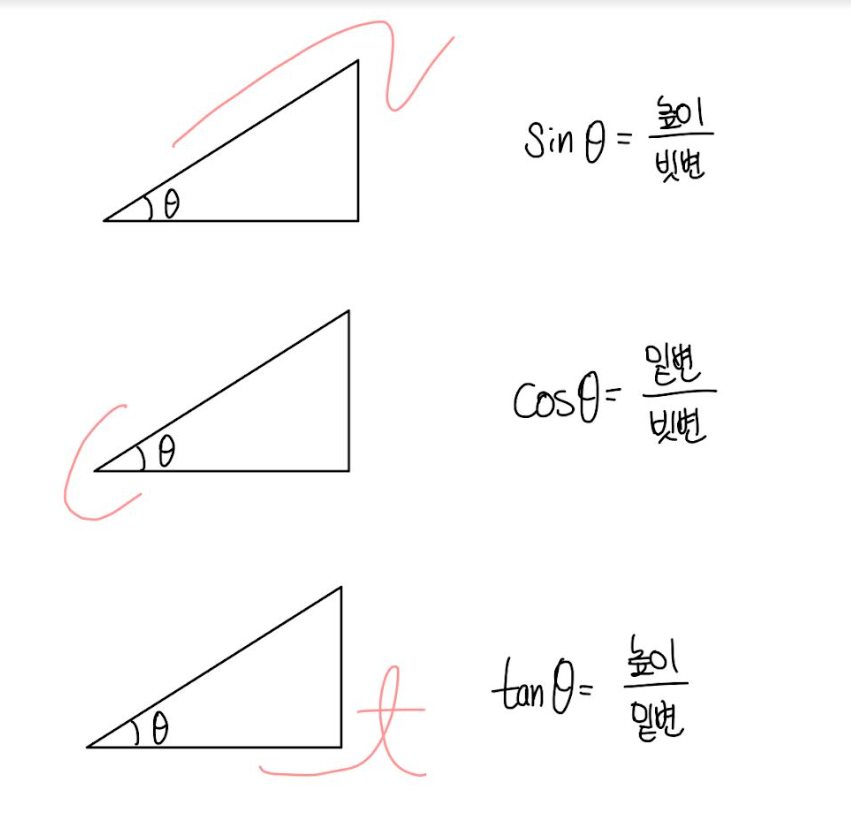
그리고 닮음인 직각삼각형끼리는 sin, cos, tan 값이 모두 같기 때문에
직각삼각형에서 직각을 제외한 어느 한 각의 크기가 정해지면 삼각형의 크기와 상관없이
그 각에 대한 삼각비 값은 일정합니다(항상 AA 닮음이 되기 때문)
2. 특수각의 삼각비
특수각의 삼각비란 어느 한 각의 크기가 30도, 45도, 60도일 때 삼각비를 의미합니다
다른 각도와 달리 위의 3개의 각도에서의 삼각비는 지금까지 배웠던 내용을 이용하여 정확한 값을 알아낼 수 있기 때문에 특수각이라고 합니다.

위와 같이 정삼각형이 있을 때 어느 한 꼭짓점에서 대변에 수선을 내리면
꼭지각을 이등분하고 변을 수직이등분 할 것입니다
정삼각형의 한변의 길이를 2a라고 하면 위 직각삼각형의 빗변의 길이는 2a, 밑변의 길이는 a(수직이등분 되었으니까),
그리고 높이는 피타고라스 정리를 이용하면 \(\sqrt{(2a)^2 - a^2} = \sqrt{3}a\)가 되겠네요
다 왔습니다!
이제 60도 각에 대한 sin, cos, tan 값을 구해보면
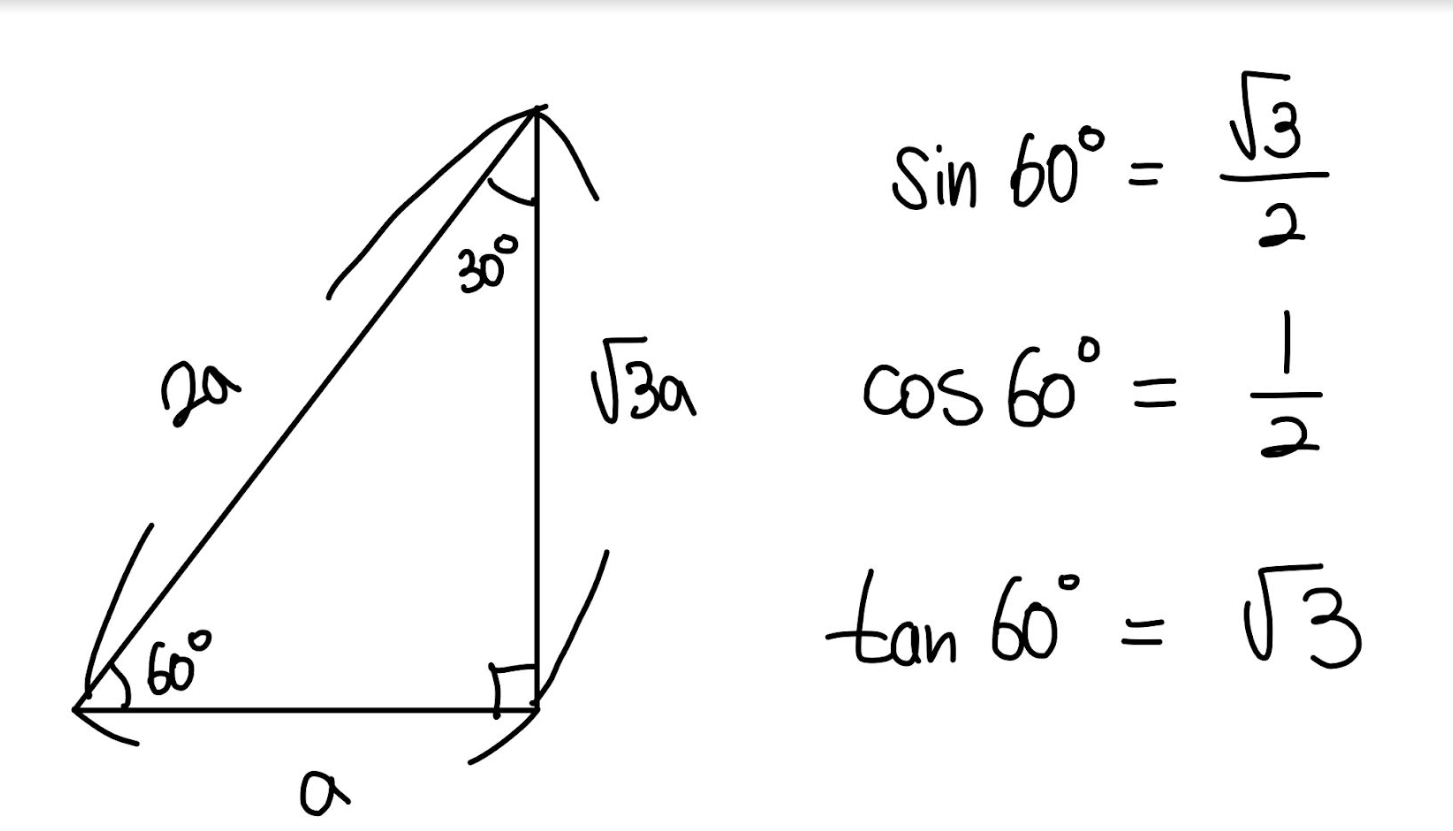
그리고 위 삼각형을 돌려서 30도 각에 대한 sin, cos, tan 값을 구해보면

그렇다면 45도에 대한 삼각비 값은 어떻게 구할까요?
직각이등변삼각형을 이용하면 됩니다
한 변의 길이를 a라고 하면 빗변의 길이는 피타고라스 정리를 이용하여 \(\sqrt{a^2 + a^2} = \sqrt{2}a\)가 되겠네요
그렇다면 45도에 대한 sin, cos, tan의 값은

이렇게 되겠네요
이를 하나의 표로 다시 정리해보겠습니다

3. 삼각비의 활용
삼각비는 각과 어느 한 변의 길이가 주어진 직각삼각형에서 다른 두 변의 길이를 알아내는 데 활용할 수 있습니다
문제를 통해 알아보겠습니다
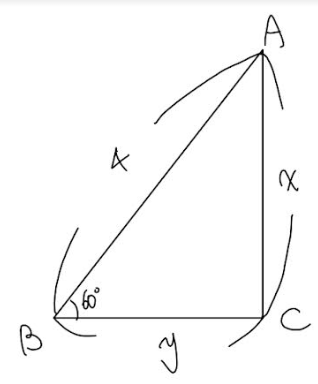
Q. 다음 삼각형에서 x, y 값을 sin, cos을 이용해 나타내고 그 값을 구하여라
풀이

그리고 삼각비는 삼각형과 사각형의 넓이를 구하는데 이용될 수 있습니다
1. 두 변의 길이와 그 사이 끼인 각의 크기가 주어진 삼각형

위 삼각형의 넓이는 \(\frac{1}{2}ab\sin\theta\) 입니다
증명은 아래와 같습니다

2. 두 대각선의 길이와 그 사이 끼인 각의 크기가 주어진 사각형

위 사각형의 넓이는 \(\frac{1}{2}ab\sin\theta\) 입니다
증명은 평행사변형의 넓이를 이용합니다

참고로 중등과정에서는 몇몇 문제를 제외하고 별로 쓸 일이 없지만 고등과정에서는 유용하게 쓰이는
두 가지 공식을 소개하고 마무리하겠습니다
\begin{equation} \tan\theta = \frac{\sin\theta}{\cos\theta} \end{equation}
\begin{equation} {\sin}^2\theta + {\cos}^2\theta = 1 \end{equation}
증명은 아래와 같습니다
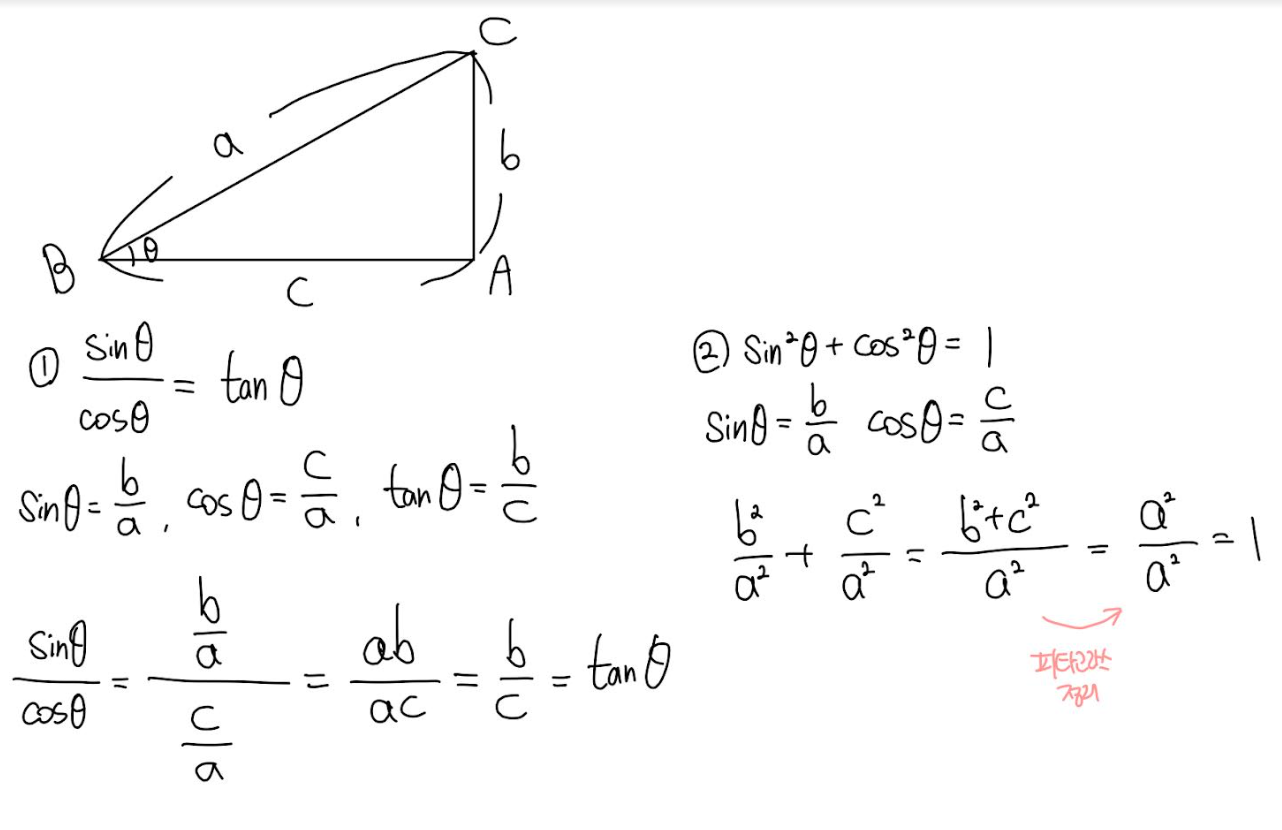
오류가 있다면 언제든지 댓글로 남겨주세요! 감사합니다
'하루 5분 중등수학' 카테고리의 다른 글
| 메넬라우스 정리와 체바의 정리 (1) | 2023.05.07 |
|---|---|
| [하루 5분 중등수학] 무리수와 실수 (0) | 2023.02.18 |
| [하루 5분 중등수학] 무리수 상등 (0) | 2023.02.13 |
| [하루 5분 중등수학] 제곱근의 곱셈과 나눗셈 증명 (3) | 2023.02.13 |
| [하루 5분 중등수학] 제곱근의 덧셈과 뺄셈 (2) | 2023.02.13 |

댓글