수학을 배워보셨다면 미분이라는 단어는 무조건 들어보셨을 겁니다
하지만 되게 어려워 보이고 글을 읽어봐도 무슨 소리인지 도통 모르겠다 하시는 분들이 계실거라 생각합니다
그래서 아래와 같은 분들을 위해 최대한 짧게 그리고 또 쉽게 미분을 설명해 보겠습니다!
1. 미분을 배우긴 했지만 개념을 아직 잘 모르겠다
2. 미분을 아직 배우지 않았지만 궁금하다
(중학생분들도 충분히 이해할 수 있을 정도로 설명했습니다)
잠깐 시작하기에 앞서 미리 공지해야 할 내용이 있습니다
이 글에서는 미분공식, 미분 문제 등을 다루지 않습니다!
단순히 미분이 무엇인지, 언제 사용하는지...등 미분을 한번도 접해보지 못한 분들을 위해
개념만 설명하는 글입니다. (이 점 참고해주세요!)
미분이란 무엇일까요?
본론부터 말하자면 미분이라는 것은 순간변화율, 즉 그래프 위 한점에서 접선의 기울기를 구하는 것입니다
식으로 나타내면 이렇게 됩니다
$$\lim_{\Delta x \to 0} \frac{f(a+\Delta x) - f(a)}{\Delta x}$$
갑자기 너무 어려운 말과 함께 처음보는 이상한 수식이 등장했습니다
오늘의 목표는 저 식을 이해하는 것입니다
자 이제부터 천천히 살펴보도록 하겠습니다!
David가 차를 타고 부산으로 여행을 가는 중이라 생각해봅시다
차를 타는 동안 차의 속력은 계속하서 변할 것입니다
David는 수학을 너무 좋아한 나머지 차의 속력이 변하는 것을 그래프로 나타내 보기로 합니다!
(왜 이런 짓을 하는지 저도 궁금합니다...)
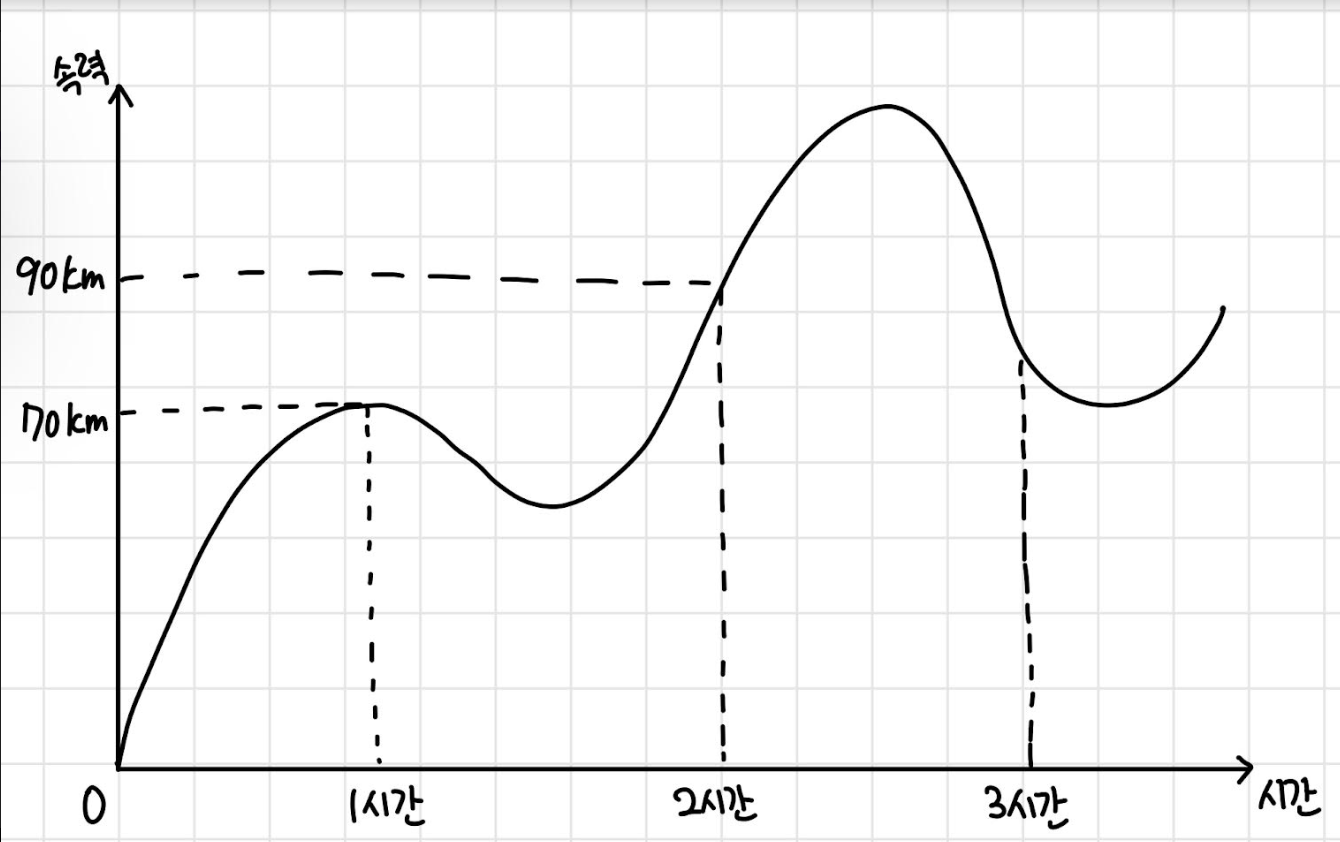
이런 식으로 나왔다고 하네요
여기서 질문 하나 드리겠습니다
이 차는 출발한지 1시간째부터 2시간이 될때 까지 속력의 평균변화율은 얼마인가요?
평균변화율? 말 그대로 해석하면 됩니다.
차의 속력이 1시간부터 2시간이 될때까지 평균적으로 얼마나 증가(또는 감소)했나요?
이것을 의미합니다(이해가...되셨나요?)
1시간 부터 2시간이 될때까지 순간순간의 속력은 계속해서 변화하고 있습니다
그렇지만! 감소하고 증가하고 이걸 다 통틀어서 평균적으로 보면 결국 1시간에 속력은 20km/h 만큼 증가했습니다
즉, 1시간부터 2시간 사이에서 평균변화율은 20이 되는 것이죠
지금까지 말한 내용을 그래프로 나타내 보겠습니다
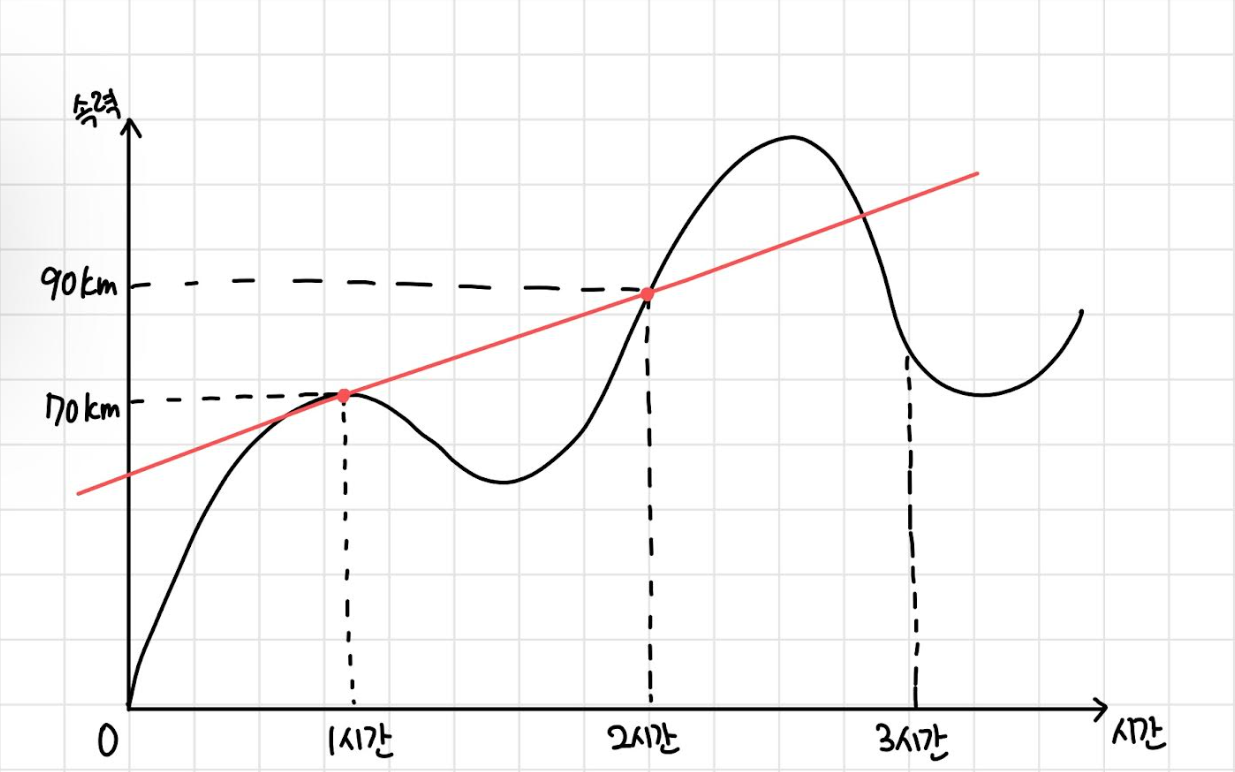
사진을 보시면 (1, 70)과 (2, 90)에 점이 찍혔고 그 두 점을 이은 직선이 하나 보입니다
이 직선의 기울기를 살펴볼까요?
기울기라는 것은 \(\frac{ y의 변화량 }{ x의 변화량} \)을 의미합니다
즉, x가 변했을 때 y는 얼마나 변했나요?를 의미하기도 하네요
이제 약간 연관성이 보이지 않나요?
위에서 우리는 시간이 1시간에서 2시간이 될때 차의 속력이 얼마나 변했는지를 구했습니다
그리고 이것이 평균변화율이라고 했었죠
그래프에서 시간은 x축, 속력은 y축이기 때문에 위의 말은 이렇게도 쓸 수 있습니다
x가 1에서 2로 변할 때 y는 얼마나 변했나요
이 말은 결국 저 직선의 기울기가 의미하는 바랑 같게 되네요!
실제로 기울기를 구해봅시다
저 직선은 (1, 70), (2, 90)을 지나기 때문에 일차함수의 기울기를 구했던 기억을 살려 구해보면
$$ \frac {90-70}{2-1} = \frac{20}{1} = 20 $$
그렇네요! 우리가 아까 구했던 평균변화율과 이 직선의 기울기는 같습니다
그럼 우리는 평균변화율을 이렇게 이야기 할 수 있겠네요
평균변화율 : x가 일정한 범위에서 변할 때 그에 따라 평균적으로 y가 변하는 정도
= 그래프 위 두 점을 지나는 직선의 기울기
이제 이것을 식으로 써봅시다
기울기라는 것은 \(\frac{ y의 변화량 }{ x의 변화량} \)을 의미합니다
이때 변화한 정도를 알고 싶으면 (나중 거)-(처음 거) 이렇게 계산해야합니다
예를 들어 x가 1부터 2까지 변화했다면 변화한 정도는 2-1 = 1이 되는 것이죠
우리는 변화한 정도를 기호로
$$\Delta x$$
이렇게 표현하기도 합니다
그럼 기울기 식도 이렇게 쓸 수 있겠네요
$$\frac {\Delta y}{\Delta x}$$
만약 \(y=f(x)\)라는 함수식이 있었고 처음 x의 값을 a라고 생각해봅시다
그러면 변화된 후의 나중 x의 값은 a + \(\Delta x\)
( \(\Delta x\) 이것이 변화된 정도를 뜻하니까요!)
이어서 y의 변화량 같은 경우 (나중 y값)-(처음 y값)이므로
$$\Delta y = f(a + \Delta x) - f(a) $$
(나중 y값은 f(x)에 나중 x값을 대입했고 처음 y값은 f(x)에 처음 x 값을 대입했습니다!)
\(\Delta y\)를 구했으니 다시 위의 기울기 식에 대입해 볼까요?
$$ \frac {f(a + \Delta x) - f(a)}{\Delta x} $$
(여러분들이 이 어려운 식을 유도해냈습니다!)
평균변화율을 설명할때는 구간이 좀 넓었습니다
1시간에서 2시간 사이였죠 (\(\Delta x = 1\))
그런데 만약 몇 초, 심지어는 0.몇초 단위로 속력이 얼마나 바뀌는지가 궁금하면 어떻게 해야할까요?
시간(x)의 변화정도가 매우 작으니까 \(\Delta x\)도 매우 작다고 할 수 있겠네요
만약 \(\Delta x\)가 계속 작아져서 0에 가까워진다면 어떨까요?
평균변화율은 두 점을 잇는 선분의 기울기였는데 \(\Delta x\)가 0에 가까워지면 두 점이 계속 가까워질테고
결국......두 점이 한 점에서 만나겠네요!
의아하신 분들이 계실겁니다. 아니 변화량이 0이 되어야 만나는 거 아니예요?
0에 가까워진다고 했지 0이 되는 건 아니잖아요
맞습니다. 엄밀히 말하자면 0이 되는 것은 아니지만 0에 한없이 가까워져서
그냥 0이라고 생각해도 될 정도로 가까워진 것입니다
(알아요, 이게 말도 안된다는 것을. 하지만 수학에서는 그냥 0에 한없이 가까워지면 0이라고 간주합니다)
그리고 이렇게 0에 한없이 가까워진다 라는 말을 기호로는
$$\lim_{x \to 0}$$
이렇게 표현합니다
어쨌든 \(\Delta x\)가 한없이 0에 가까워지면 두 점이 한 점에서 만나기 때문에
이때 직선은 그래프와 한점에서 만나겠네요
한점에서 만난다는 것은? 그래프와 직선이 접한다는 뜻이겠네요!
그리고 이때의 기울기는 평균변화율이라 하지 않고 엄청 짧은 구간에서의 변화율이기 때문에 순간변화율이라고 합니다.
정리해보면 순간변화율이라는 것은 \(\Delta x\)가 0에 한없이 가까워질 때의 평균변화율이네요
그러면 \(\Delta x\)가 0에 가까워진다 + 평균변화율 =
$$\lim_{\Delta x \to 0} \frac{f(a+\Delta x) - f(a)}{\Delta x}$$
이렇게 식으로 쓸 수 있는 것이죠
위 식이 바로 순간변화율을 구하는 식입니다
(아래 그림 초록색 직선 참고)
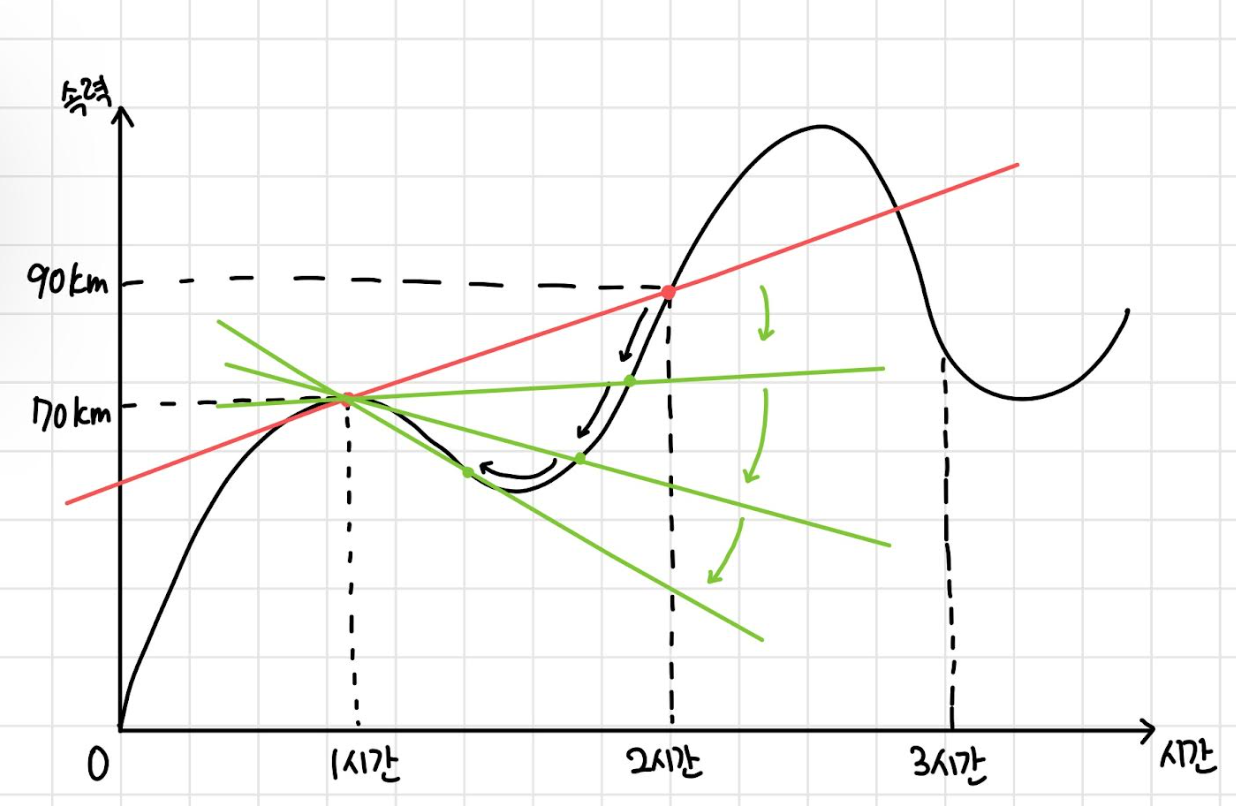
\(\Delta x\)가 0에 한없이 가까워 질때 점의 위치와 기울기의 변화

\(\Delta x\)가 한없이 0에 가까워져 결국 두 점이 만났을 때의 기울기(이때가 직선의 기울기가 순간변화율입니다)
순간변화율, 그래프와 직선이 접할 때의 기울기, 그리고 저 식......
잠깐만요, 이 글의 맨 위로 돌아가보면
미분이라는 것은 순간변화율, 즉 그래프 위 한점에서 접선의 기울기를 구하는 것이다
라고 제가 소개했었습니다
맞아요, 지금 설명드린 바로 이 개념이 미분입니다!
x = a에서 순간변화율, 그래프와 접하는 직선의 기울기가 바로 이거입니다
$$\lim_{\Delta x \to 0} \frac{f(a+\Delta x) - f(a)}{\Delta x}$$
여러분들은 이제 저 식이 무엇을 의미하는 지 알게 되었습니다
중학생들도 이해할 수 있도록 글을 쓰다 보니 극한의 대한 개념, 함수의 연속 같은 내용들은 빼고 설명했습니다
추후에 수2 내용 정리 할 때, 그때는 자세하게 다뤄보도록 하겠습니다
오류가 있다면 언제든지 댓글로 알려주세요
긴 글 읽어주셔서 감사합니다!
'하루 5분 수학이야기' 카테고리의 다른 글
| [하루 5분 수학이야기] 로또에 당첨될 확률은? (0) | 2023.03.12 |
|---|---|
| [하루 5분 수학이야기] 이진법이란 무엇일까? (0) | 2023.03.05 |
| [하루 5분 수학이야기] 100의 99제곱 vs 99의 100제곱 누가 더 클까? (0) | 2023.02.24 |

댓글