3월 23일에 올해 첫 모의고사가 있었습니다
이번 글에서는 고1 3월 모의고사 수학 최다 오답률 문제에 대한 풀이과정을 공유해볼까 합니다
(오답률은 ebs에서 참고했습니다)
오답률 3위 : 21번 문제 (오답률 79.3%)

이 문제는 내심의 성질을 종합적으로 이용해야 되는 문제입니다
먼저 ㄱ 부터 보겠습니다
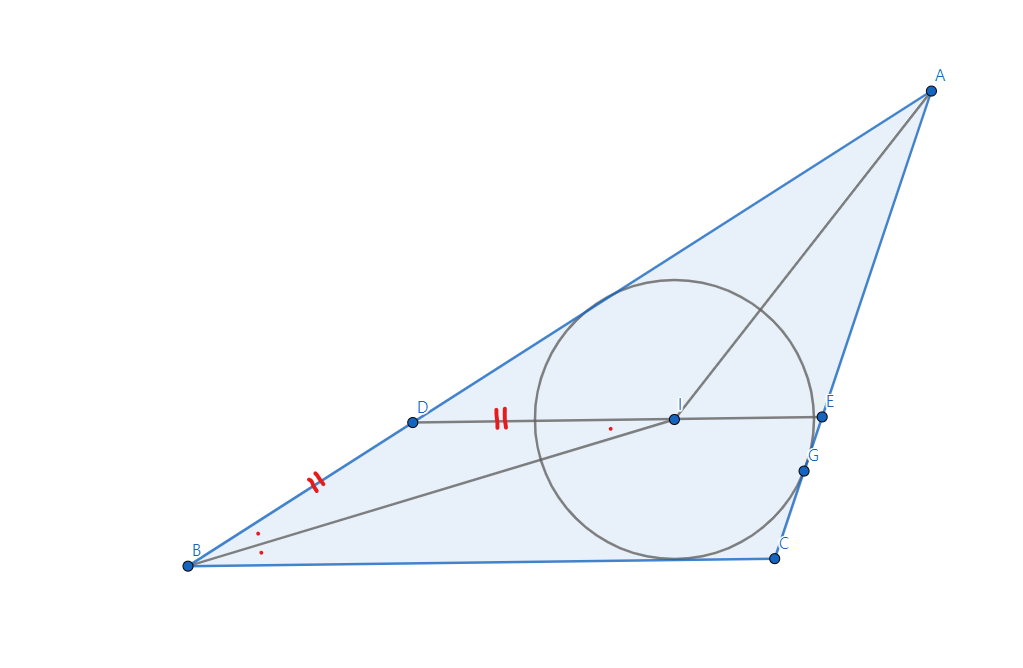
ㄱ 에서 \(\angle BID = \angle IBD\)라고 했는데
내심의 성질에 의해 선분 BI는 각 B를 이등분합니다
그리고 선분 DE 와 BC가 평행하다고 했으니(문제에 나와있습니다)
엇각의 성질에 의해 \(\angle IBC = \angle BID = \angle IBD\)
다음은 ㄴ 입니다
삼각형 ADE의 둘레가 \(7\sqrt{2}\)라고 하네요

F, G, H는 원과 삼각형이 만나는 접점입니다
원의 중심에서 접점에 선분을 이으면 수직이므로 삼각형 AFI는 직각삼각형입니다
문제에서 선분 AI의 길이가 3이고 내접원의 반지름은 1이기 때문에 피타고라스 정리에 의해
선분 AF의 길이는 \(2\sqrt{2}\)입니다
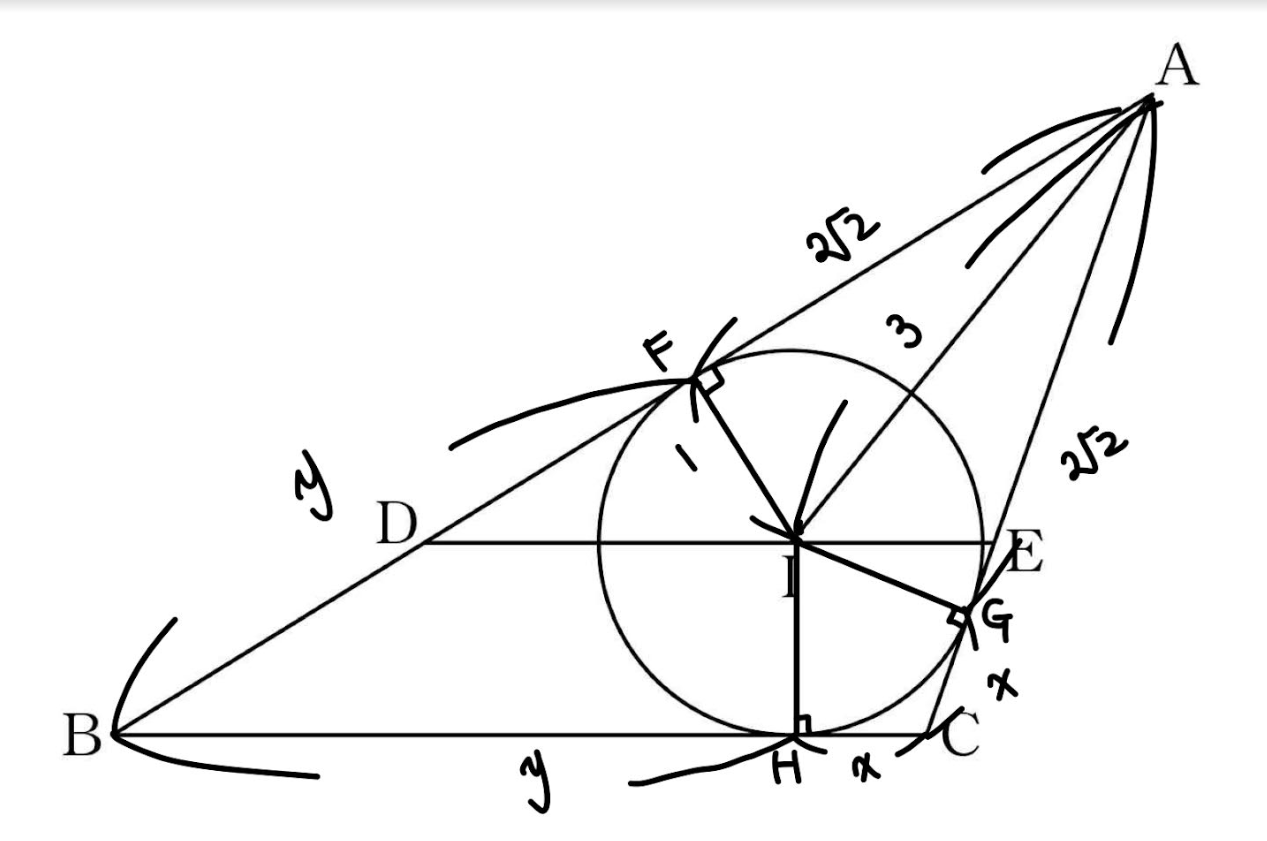
원 밖의 한점에서 원에 접선을 그리면 그 두 접선의 길이는 같다는 성질을 이용하면
선분 AG도 \(2\sqrt{2}\)인 것을 알 수 있습니다
그리고 CG = x, BF = y 라고 한다면
역시나 같은 원리로 CH = x, BH = y가 됩니다
문제에서 삼각형 ABC의 넓이가 \(5\sqrt{2}\)라고 했으므로
삼각형 ABC의 넓이 = \(\frac{1}{2} \times 내접원의 반지름 \times 삼각형 ABC의 둘레\)
라는 공식을 이용해준다면
삼각형 ABC의 둘레가 \(10\sqrt{2}\)라는 결론이 나옵니다
삼각형 ABC의 둘레는 결국
\(2\sqrt{2} \times 2 + 2x + 2y = 10\sqrt{2}\)이므로 \(x + y = 3\sqrt{2}\)입니다
ㄱ에서 삼각형 DBI가 이등변삼각형이라는 것을 증명했습니다
즉 DB = DI라는 것이죠
그렇다면 같은 원리로 삼각형 EIC도 이등변 삼각형이고 EI = EC입니다
결국 삼각형 ADE의 둘레 = AB + AC = \(2\sqrt{2} \times 2 + x + y = 7\sqrt{2}\)
ㄷ은 비교적 쉽게 증명이 가능합니다

여기서 DE와 BC가 평행하기 때문에
삼각형 ADE와 삼각형 ABC는 닮음입니다
그런데 아까 ㄴ에서 증명했던 것 처럼
삼각형 ABC의 둘레는 \(10\sqrt{2}\)이고 삼각형 ADE의 둘레는 \(7\sqrt{2}\)입니다
결국 닮음비는 둘레비랑 같기 때문에 둘의 닮음비는 10 : 7이 되는 것이죠
그리고 BC = x + y = \(3\sqrt{2}\)
결국 DE : \(3\sqrt{2}\) = 7 : 10
DE = \(\frac{21\sqrt{10}}{10}\)
ㄷ은 틀리네요
결국 정답은 ㄱ,ㄴ 2번이네요
오답률 2위 : 29번 문제 (오답률 88.7%)

일단 하나하나 주어진 조건을 그림에다 옮겨보겠습니다

구하려는 삼각형 EDG의 넓이를 S라고 놓았습니다
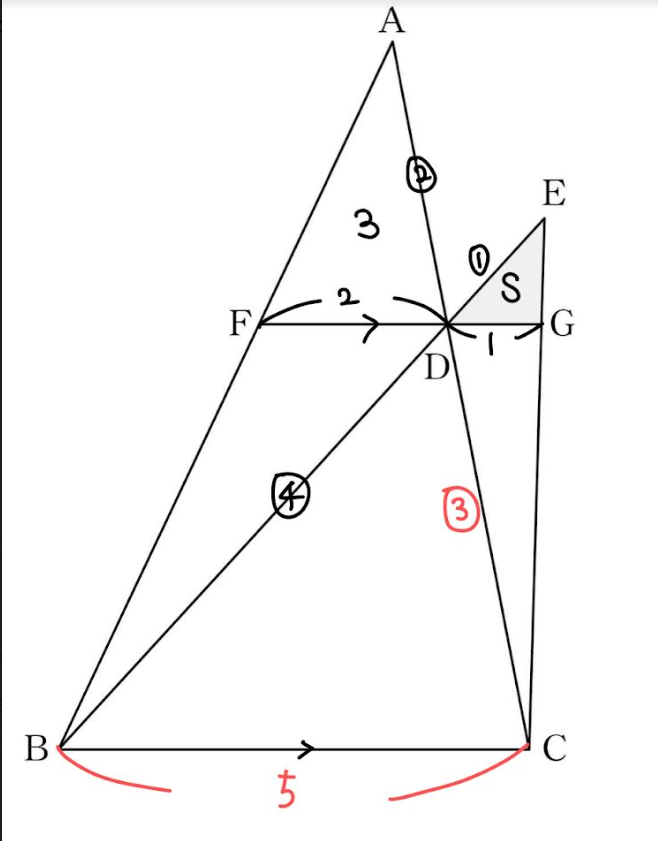
삼각형 EDG와 EBC는 닮음이고 닮음비는 1: 5입니다
즉 선분 BC의 길이는 5가 됩니다
그리고 이때 삼각형 AFD와 ABC 역시나 닮음이고 닮음비는 2 : 5가 됩니다
결국 선분 AD : 선분 DC = 2 : 3 입니다

이제 본격적으로 넓이를 살펴봅시다
ED : BD = 1 : 4이니 EG : GC 도 1 : 4입니다
삼각형 EDG : 삼각형 DCG = 1 : 4
삼각형 DCG = 4S
(높이가 같으면 넓이비는 밑변의 길이비)
삼각형 EDC : 삼각형 DBC = 1 : 4
삼각형 DBC = 20S

AD : DC = 2 : 3이므로
삼각형 ABD : 삼각형 DBC = 2 : 3
이때 삼각형 DBC = 20S이기에
삼각형 ABD : 20S = 2 : 3
삼각형 ABD = \(\frac{40}{3}S\)입니다
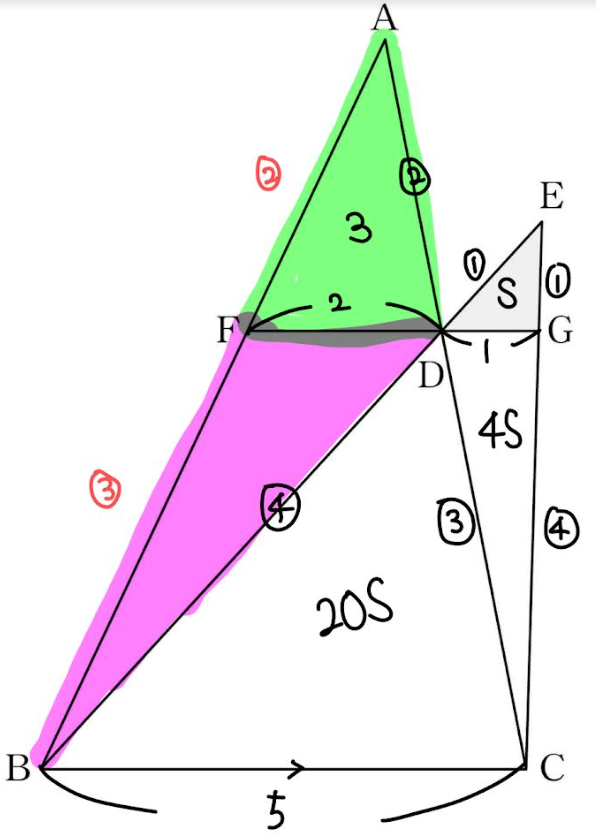
삼각형 ABD = \(\frac{40}{3}S\)이고
삼각형 AFD : 삼각형 FBD = 2 : 3
결국 삼각형 AFD = \(\frac{40}{3}S \times \frac{2}{5} = \frac{16}{3}S\)
그런데 문제 조건에서 삼각형 AFD의 넓이가 3이라고 했으므로
$$\frac{16}{3}S = 3$$
$$S = \frac{9}{16} $$
결국 p + q = 25
오답률 1위 : 30번 문제 (오답률 91.3%)

무려 오답률이 90%가 넘어가는 문제입니다
일단 가장 먼저 주어진 조건을 문제에 표시해 보겠습니다

선분 AB = 선분 BC이므로
호 AB = 호 BC입니다
호의 길이가 같다면 원주각의 크기도 같기 때문에
\(\angle ADB = \angle CDB\)
각이 같다는 것을 표시하기 위해 동그라미로 표시해 두었습니다
그리고 삼각형 ADE와 삼각형 CDE는 ASA합동이기 때문에
선분 CE = x, 선분 AD = 선분 CD 입니다
그리고 원 밖의 한점에서 원에 그은 두 접선의 길이는 같기 때문에 FC = 2입니다
결국 삼각형 ADC와 삼각형 FDC는 이등변삼각형입니다
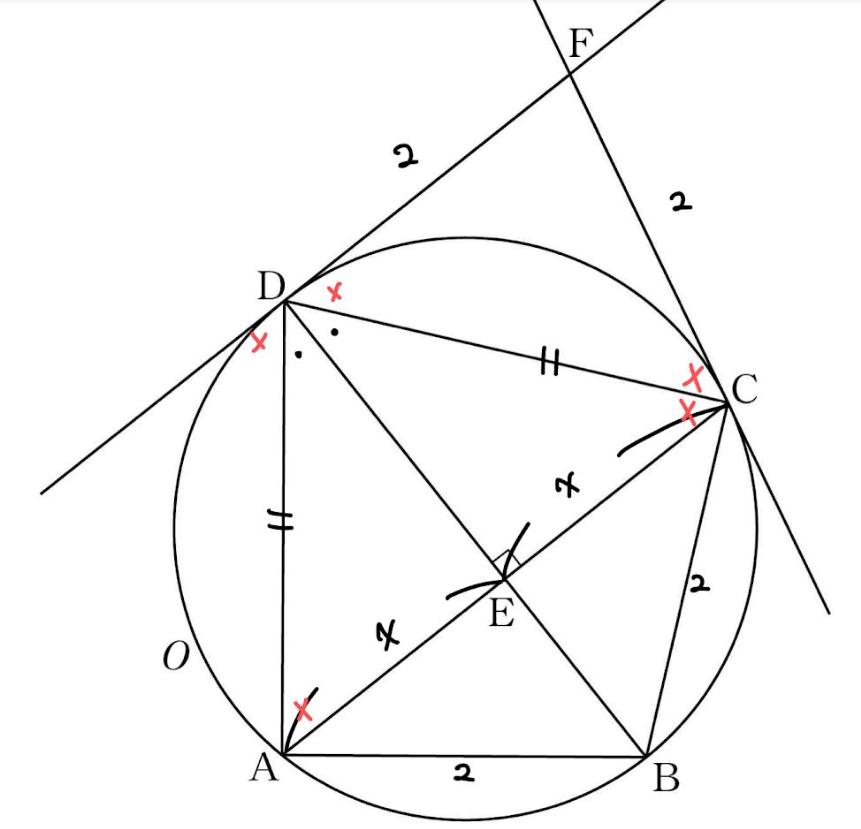
\(\angle DAE\)를 x 라고 해보겠습니다
그러면 (각) o + x = 90도입니다
그리고 삼각형 ADC는 이등변삼각형이라고 했기 때문에 \(\angle DCE\) = x 입니다
접현각 성질에 의하여 \(\angle DAC = \angle CDF\)입니다
그리고 삼각형 FDC는 이등변삼각형이기에 \(\angle CDF = \angle FCD\)

이제 이 문제에서 가장 중요한 포인트를 살펴보겠습니다
위의 조건을 통해 닮음을 찾을 수 있습니다
바로 삼각형 DAC와 삼각형 FDC가 AA닮음이죠!
그렇다면 닮음비를 이용하여 비례식을 세워보겠습니다
선분 DC : \(2x\) = 2 : 선분 DC
\({DC}^2 = 4x\)
$$ DC = 2\sqrt{x} $$

호 AB에 대한 원주각인 \(\angle ADB = \angle ACB\)
(각) o + x = 90도 이기 때문에
\(\angle DCB = 90\)
삼각형 DBC는 직각삼각형이고 피타고라스 정리를 이용한다면
$$ {DB}^2 = {DC}^2 + {CB}^2 $$
$$ {DB}^2 = 4x + 4 $$
$$ DB = 2\sqrt{x+1} $$
거의 다 왔습니다
삼각형 DBC에서 다음이 성립합니다
$$ CD \times CB = DB \times CE $$
방정식은 사진으로 대체하겠습니다

이렇게 이번 고1 3월 모의고사 최다 오답 문제 Top3를 풀어보았습니다
오류가 있다면 언제든지 댓글로 남겨주세요 감사합니다!
댓글